проект учащихся 5 класса «Задачи на части»
учащиеся сами составляли задачи на части и оформили это в виде сборника задач.
Скачать:
| Вложение | Размер |
|---|---|
| sbornik_zadach_na_chasti.doc | 72 КБ |
Предварительный просмотр:
Сборник задач на части.
Авторы-составители учащиеся 5 класса
Если вы хотите научиться плавать,
то смело входите в воду,
а если хотите научиться решать задачи,
- Введение.
- Задачи от Кирсановой Елизаветы.
- Задачи, которые составил Анашкин Никон.
- Свои задачи предлагает Варюхина Юлия.
- Необычные задачи Колдина Егора.
- Комментарии. Выводы.
В повседневной жизни человеку нередко приходится сталкиваться с «рецептами» приготовления (или изготовления чего-либо), в составе которых указаны части. Такие задачи встречаются в кулинарии, в химической промышленности, медицине, особенно в фармацевтической промышленности. И, взрослые, решая эти задачи, наверное и не задумывались, что всех их можно объединить в один вид математических задач- «Задачи на части».
Мы , 5- классники, уже познакомились с такими задачами на уроках математики.
Нам встречались, например, такие задачи:
Задача 1. Для приготовления состава для полировки берут 5 частей нашатырного спирта,
2 части мела и 10 частей воды. Сколько грамм каждого вещества нужно взять, чтобы получить 540 г полировки?
Задача 2 . Настойка для полоскания рта содержит:
ромашки — 3 части, календулы — 2 части,
шалфея — 4 части. Сколько грамм настоя получится, если ромашки взять 210 г.?
Задача 3 . Для приготовления варенья из ягод используют классический рецепт: на 3 части ягод берут 2 части сахара. Сколько килограммов сахара надо купить, чтобы сварить варенье из 9 килограммов ягод?
Если вы уже учитесь в 5 классе и знаете как решаются задачи на части, то вы без труда сможете решить эти три задачи.
После этого приступайте к решению наших задач.
Смелее и у вас все получится. Желаем успехов!
2. Задачи от Кирсановой Елизаветы.
№1 . Одну часть всего урожая составляет свёкла, а картофель – 2 части. Сколько кг собрали свёклы и сколько картофеля, если всего собрали 2 т 700 кг овощей?
№2 . Для варки варенья из вишни нужно взять 2 части ягод и 3 части сахара. Сколько кг сахара потребуется на 10 кг ягод?
№3. К Новому году мама купила елочные украшения на сумму 560 рублей. Оказалось, что елочные бусы дороже набора елочных шаров в 3 раза. Сколько стоит каждое украшение в отдельности?
№4 . Елочная гирлянда дороже рождественской звезды в 3 раза. Сколько стоит вся покупка, если за гирлянду заплатили на 160 руб больше?
3.Задачи, которые составил Анашкин Никон.
№1. Задачи из кулинарии.
Для того, чтобы сварить 500 г овсяной каши, берут 2 части овсяных хлопьев и 3 части воды. Сколько грамм овсяных хлопьев нужно взять для приготовления 2 кг каши?
№2. «Строительная» задача.
Для кирпичной кладки готовят раствор из 4 ч. глины, 1ч. песка и 2 ч. воды. Сколько кг. Раствора получим, если воды возьмем 1 кг 800 г?
4.Свои задачи предлагает Варюхина Юлия.
Скоро Новый год и я составила «новогодние» задачи.
№1 . Мама и сын стали наряжать ёлку. Когда они стали вешать на елку гирлянды, то обнаружили, что на одной из них в 2 раза фонариков больше. Сколько фонариков на каждой гирлянде, если на двух вместе 90 фонариков?
№2. Таня, Вика и Света пошли в магазин покупать новогодние игрушки. Они решили купить все одинаковые шары по цене 24 руб . У Тани оказалось в 2 раза больше денег, чем у Вики, а у Светы столько, сколько у Тани и Вики вместе. Когда они сложили все деньги, то у них оказалось 288 руб. Сколько новогодних шаров будет у каждой девочки?
5.Необычные задачи Колдина Егора.
№1. «Вкусная» задача.
Для детских новогодних подарков было куплено
60 кг мармеладных конфет с арбузом и персиком.
Но с арбузом купили в 3 раза больше, чем с персиком.
Сколько кг конфет каждого сорта было куплено?
В трех коробка 55 кусков пластилина. Когда из одной израсходовали 7 кусков, то в ней осталось в 2 раза меньше, чем в другой и в 3 раза меньше, чем в третьей. Сколько кусков пластилина было в коробках первоначально?
В преддверии новогодних праздников, мы вдохновились этой темой и составили 5 задач на части новогодней тематики. Надеемся, что они вам понравились и не очень сложные. Также мы привели примеры задач из области кулинарии, строительства.
И это далеко не все области решения и применения задач на части.
Из литературы, которую мы изучали по этой теме, мы уяснили, что такие задачи нам будут встречаться на протяжении всего изучения математики в школе, но уже более сложные, и даже с дробями. После этой работы мы готовы к новым испытаниям!
Источник
Задачи на части.
тренажёр по математике (5 класс)
Разноуровневые задачи на части в 5 классе.
Скачать:
| Вложение | Размер |
|---|---|
| zadachi_na_chasti_5_klass.docx | 17.17 КБ |
Предварительный просмотр:
Одним из сложных разделов математики является решение задач
Сложным он является потому что для решения задач учащемуся необходимо иметь навык логического мышления, умения устанавливать связь в предметах и дейсвиях, понимать смысл текста (условия задачи). Если учащийся не осмыслил условие задачи, то, естественно, и решить ее он не сможет.
Решение задач на части 5 класс.
Задача 1 . В кулинарной книге написано, что для варенья из малины нужно на 3 части ягод взять две части сахара. Сколько сахара нужно взять на 9 кг ягод?
Решение: т.к. 9 кг ягод составляют 3 части, то можно узнать: сколько
килограммов приходится на 1 часть?
Сахар должен составлять 2 части, следовательно, сахара нужно взять
Задача 2. Для детских новогодних подарков были закуплены шоколадные конфеты и карамель – всего 20 кг. Сколько было закуплено конфет того т другого сорта, если карамели взяли в 3 раза больше, чем шоколадных конфет?
Решение: Это тоже задача на части, только их нужно специально ввести. Будем
считать, что шоколадные конфеты составили 1 часть, тогда карамель
составила 3 части.
Всего на 20 кг конфет приходится 1 + 3 = 4 (части), следовательно:
20 : 4 = 5 кг
тогда
5 ∙ 1 = 5 кг – шоколадных конфет
5 ∙ 3 = 15 кг – карамели
Задача 3. Длины сторон треугольника относятся как 3:4:5. Вычислить длину каждой стороны, если периметр треугольника 48 см.
Решение: Соотношение сторон 3:4:5 означает, что одна сторона – 3 части,
вторая – 4 части, третья – 5 частей. т.о. Находим количество частей:
3 + 4 + 5 = 12
Далее считаем, сколько см приходится на 1 часть (периметр – это
сумма длин всех сторон)
48 : 12 = 4 см
т.о. одна сторона (3 части) – 3 ∙ 4 = 12 см,
вторая сторона (4 части) – 4 ∙ 4 = 16 см,
третья сторона (5 частей) – 5 ∙ 4 = 20 см
Задачи: Уровень А
- Для варенья из вишни на 2 части ягод берут 3 части сахара
а) Сколько сахара следует взять для 2600 г ягод?
б) Сколько кг вишни было у мамы, если для варки варенья она приготовила
4 кг 500 г сахара? - Требуется смешать 3 части песка и 2 части цемента. Сколько цемента и песка
нужно взять отдельно, чтобы получить 30 кг смеси? - Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши
3 части, сливы 2 части общего веса всех фруктов. Сколько граммов яблок,
груш и слив было в отдельности? - Яблоки составляют 7 частей, груши 4 части, сливы 5 частей общего веса
сухофруктов. Найдите общий вес сухофруктов, если в них содержится 160 г
груши? - При пайке изделий из жести применяют сплав, содержащий 2 части свинца и
5 частей олова
а) Кусок сплава весит 350 г. Сколько в нем содержится свинца и сколько
олова?
б) Сколько свинца и олова содержит кусок сплава, в котором олова на 360 г
больше, чем свинца? - При помоле на каждые 3 части муки получается 1 часть отходов. Сколько
смололи ржи, если муки получилось на 36 ц больше, чем отходов? - Взяли 6 частей яблок, 5 частей груш и 3 части слив. Груш и слив вместе
2 кг 400 г. Сколько всего сухофруктов?
- Купили 60 тетрадей, причем тетрадей в клетку было в 2 раза больше, чем
тетрадей в линейку. Сколько частей приходится на тетради в линейку; на
тетради в клетку; на все тетради. Сколько купили тетрадей в клетку,
сколько в линейку? - На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках
вместе – 420 книг. Сколько книг стояло на каждой полке? - За рубашку и галстук папа заплатил 140 руб. Рубашка дороже галстука
в 4 раза. Сколько стоит галстук? - В плацкартном вагоне в 3 раза больше спальных мест, чем в мягком вагоне.
Всего в этих вагонах 72 места. Сколько спальных мест в мягком вагоне? - Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 орехов.
Девочка сорвала в 2 раза меньше мальчика. Сколько орехов сорвала
девочка? Сколько мальчик? - Девочка прочитала в 3 раза меньше страниц, чем ей осталось прочитать.
Всего в книге 176 страниц. Сколько страниц прочитала девочка? - Надо разложить в два пакета 56 орехов так, чтобы в одном было в 3 раза
больше, чем в другом. Сколько орехов надо положить в каждый пакет? - В отрывном календаре 366 листов. К сентябрю в календаре осталось листов в
2 раза меньше, чем оторвали. Сколько листов оторвали? - Ученик купил тетрадей в клетку в 3 раза больше, чем тетрадей в линейку.
Причем их было на 18 больше, чем тетрадей в линейку. Сколько тетрадей
купил ученик? - На первой полке стояло в 4 раза больше книг, чем на второй. Это на 12 книг
больше, чем на второй полке. Сколько книг стояло на каждой полке? - За три дня Митя прочитал 84 страницы. В первый день он прочитал в 3 раза
больше чем во второй, а в третий – 16 страниц. Сколько страниц прочитал
Митя в первый день? - Кусок ткани длиной 76 м разрезали на 3 части. Первая из них имеет длину
25 м, а вторая в 2 раза короче третьей. Найдите длину второй и третьей
части. - Дочка младше мамы в 4 раза и младше бабушки в 9 раз. Сколько лет
каждой, если вместе им 98 лет? - У Сережи в коллекции в 3 раза меньше марок, чем у Васи, а у Андрея
в 2 раза больше, чем у Васи. Сколько марок у каждого, если у Андрея
на 80 марок больше, чем у Сережи? - В двух коробках 36 кусков мела. Когда из одной коробки израсходовали
12 кусков мела, то в ней стало в 3 раза меньше мела, чем в другой. Сколько
кусков мела было в каждой коробке первоначально? - В двух банках 5 л молока. Когда в одну банку добавили 1 л, то в ней стало в 2 раза больше молока, чем в другой. Сколько литров молока было в каждой банке первоначально?
- В трех больших пакетах и четырех маленьких содержится 550 г печенья. Сколько граммов в маленьком пакете, если в него входит в 2 раза меньше печенья, чем в большом?
- В шести маленьких коробках на 12 карандашей больше, чем в двух больших. Сколько карандашей во всех маленьких коробках и сколько во всех больших, если в одной маленькой коробке в 2 раза меньше карандашей, чем в большой?
Источник
Задачи «на части» в 5-м классе, на ВПР и итоговых экзаменах
Если вы решили заниматься летом с ребёнком математикой, но с трудом вспоминаете школьную программу, наш блогер Александр Шевкин поможет вам всё наверстать. Сегодня он приводит примеры задач «на части» и объясняет, как их решать.
Задачи «на части» являются классическим типом задач, решаемых как арифметически, так и при помощи уравнения. Такие задачи встречаются в учебниках для пятого класса, в ВПР и на выпускном экзамене.
Для развития мышления и речи детей начинать лучше с арифметического способа решения. Рассмотрим решения двух задач из учебника «Математика, 5» (Просвещение, С. М. Никольский и др.) В первых задачах части упоминаются явно.
Задача 1. Для варенья из малины на 2 части ягод берут 3 части сахара. Сколько сахара следует взять на 6 кг ягод?
Решение: По условию задачи ягод 6 кг, и это количество составляет 2 части, поэтому на каждую часть приходится:
Сахара надо взять 3 такие же части, то есть:
В следующей задаче некоторую величину надо принять за одну или несколько равных частей. При решении таких задач полезно рисовать схематические рисунки, облегчающие решение.
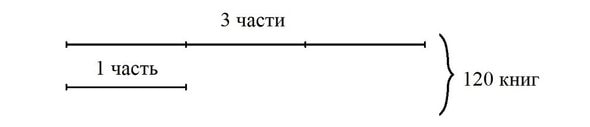
Задача 2. На двух полках стоит 120 книг — на первой полке в 3 раза больше, чем на второй. Сколько книг стоит на каждой полке?
Решение: Если книги, стоящие на второй полке, составляют 1 часть, то на первой полке — 3 такие части. Выполним схематический рисунок.
1) Сколько частей составляют 120 книг?
2) Сколько книг приходится на 1 часть?
3) Сколько книг приходится на первую полку?
Ответ: 90 и 30 книг.
Следующая задача была предложена на экзамене «Математическая грамотность» (Казахстан). Это аналог нашего ЕГЭ базового уровня для выпускников средней школы.
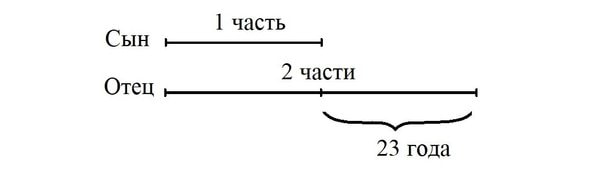
Задача 3. Когда отцу был 31 год, сыну было 8 лет. Сейчас отец в 2 раза старше сына. Сколько лет сыну сейчас?
Решение: Отец старше сына на 31 — 8 = 23 года. Пусть сейчас возраст сына составляет 1 часть, тогда возраст отца — 2 такие же части. Выполним схематический рисунок.
Замечание. Эту задачу преподаватель из ютьюба, обучавший выпускников казахстанских школ, решал при помощи уравнения, приняв за x число лет, прошедших между описанными в задаче событиями.
В заключение задача посложнее.
Задача 4. Для компота купили 1800 г сухофруктов. Яблоки составляют 4 части, груши 3 части, а сливы 2 части общего веса сухофруктов. Сейчас граммов яблок, груш и слив было в отдельности?
1) 4 + 3 + 2 = 9 (частей) — приходится на 1800 г,
2) 1800: 9 = 200 (г) — приходится на 1 часть,
3) 200 ∙ 4 = 800 (г) — было яблок,
4) 200 ∙ 3 = 600 (г) — было груш,
5) 200 ∙ 2 = 400 (г) — было слив.
Ответ: 800, 600 и 400 г.
Отметим, что приём решения задач «на части» может использоваться при решении более сложных составных задач.
Задача 5. На двух полках стояли 36 книг. Когда с первой полки на вторую переставили 3 книги, то книг на второй полке стало в 2 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?
Решение: Пусть количество книг на первой полке после перестановки трёх книг составляет 1 часть, тогда на второй полке — 2 части.
1) 1 + 2 = 3 (части) — приходится на 36 книг,
2) 36: 3 = 12 (книг) — приходится на 1 часть (стало на 1-й полке),
3) 36 — 12 = 24 (книг) — стало на 2-й полке.
Вернём три книги на первую полку.
4) 12 + 3 = 15 (книг) — было на первой полке первоначально,
5) 24 — 3 = 21 (книга) — была на второй полке первоначально.
Ответ: 15 и 21 книга.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Источник